Section 2.7: TEM Mode, Beam Diameter, Focal Spot Size and Depth of Focus
Modes are the standing oscillating electromagnetic waves which are defined by the cavity geometry. In the above section, we already computed the Longitudinal Modes frequencies for some simple cases. If the cavity is of closed form, i.e., both the mirrors and side walls are reflective, there will be large amounts of longitudinal modes oscillating inside the cavity, a typical value can be 109 modes for a He-Ne laser. People had thought closed form could improve the output power, but it turns out that the output beam can not be well focused for closed cavities with so many modes. So open oscillators are used, whose lateral walls are not reflective, light incident on this part will be absorbed. This can reduce the possible longitudinal modes to only a few, for example, as low as 6!
When these modes oscillate, they interfere with each other, forming the transverse standing wave pattern on any transverse intersection plane. This mechanism decides the Transverse Electromagnetic Modes (TEM) of the laser beam, which is the wave pattern on the output aperture plane. We use the sign TEMpql to specify a TEM mode, where p is the number of radial zero fields, q is the number of angular zero fields, q is the number of longitudinal fields, and we usually use TEMpq to specify a TEM mode, without the third index. A table of TEM patterns is shown below. Clearly, the mode pattern affects the distribution of the output beam energy, which will thus affect the machining process.
Then what is the diameter of a laser beam? Usually this diameter is defined as the distance within which 1/e2 of the total power exists.
The higher the order of the mode, the more difficult it is to focus the beam to a fine spot, since the beam of higher order is not from a virtual point, but from patterns as those in the table below.

Table 2.14: Table of modes
Focal Spot Size:
Focal spot size determines the maximum energy density that can be achieved when the laser beam power is set, so the focal spot size is very important for material processing.
When a beam of finite diameter D is focussed by a lens onto a plane, the individual parts of the beam striking the lens can be imagined to be point radiators of new wave front. The light rays passing through the lens will converge on the focal plane and interfere with each other, thus constructive and destructive superposition take place, light energy is distributed as described in figure????? below. The central maximum contains about 86% of the total power.
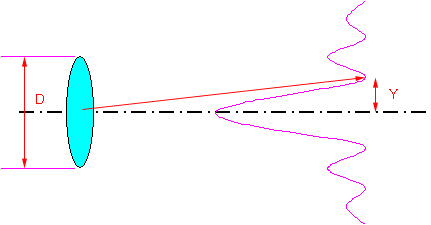
Figure 2.15: Focus pattern of parallel light
The focusing diameter is measured between the points where the intensity has fallen to 1/e2 of the central peak value. For a rectangular beam with a plane wave front, the diffraction limited beam diameter, which is the smallest focal diameter, is given by:
dmin = fl /D
For a circular beam, the equation is:
dmin = 2.44fl /D, you can try the interactive figure below to see the influnce of l and D on dmin.
For multi-mode beam TEMplq, the focal spot size is larger than the above two values. The smallest possible focal sopt size in this case is:
dmin = 2.44fl (2p+l+1)/D
Where f is the lens focal length, D is the beam diameter, l is wavelength of the light, p, l is the mode number. From this equation, we can clearly see the influence of modes to the focal property.
There are other factors that affect focal spot size, such as spherical aberration and thermal lensing effects. Most lenses are made with a spherical shape, but they cannot be of perfect shape, there exist spherical aberration. Lenses in laser systems transmit or reflect high power laser radiation, laser power variations can cause shape changes of the lenses, so the focal point will change when the radiation power changes, thus affect the focal spot size.
We prefer small focal spot size. We find the focal diameter is related to beam mode, wavelength, beam diameter and focus. How do they affect the focal spot size? You can try!
G2.8: Relations between wavelength, input beamsize and Minimum Focal Spot Size
Depth of Focus (DOF):
The laser light is first converged at the lens focal plane, then diverges to wider beam diameter again. The depth of focus is the distance over which the focussed beam has about the same intensity, it is defined as the distance over which the focal spot size changes –5%~5%. The equation for DOF is:DOF=(8l /p )(f/D)2=2.44l (f/D)2
Where l is the wavelength, f is the lens focal length, D is the unfocussed beam diameter.
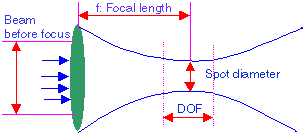
Figure 2.16: The DOF (Depth of Focus) of laser light
Usually longer depth of focus is preferred, because equal energy density along the beam is preferred when using the laser to process materials.