The most widely used laser resonators or cavities have either plane or spherical mirrors of rectangular or circular shape, separated by some distance L. There have appeared Plane Parallel Resonators, Concentric (Spherical) Resonators, Confocal Resonators, Generalized Spherical Resonators and Ring Resonators.

Plane Parallel Resonator consists of two plane mirrors set parallel to each other, as shown in the figure below. The one round trip of wave in the cavity should be an integral number times 2p , the resonant frequencies is n = kc/(2L), k is an integral number, c is the speed of light in the medium, L is the cavity length. The frequency difference between two consecutive modes (possible standing wave in the cavity) is c/(2L). This difference is referred to as the frequency difference between two consecutive longitudinal modes; the word longitudinal is used because the number k indicates the number of half-wavelengths of the mode along the laser resonator, i.e., in the longitudinal direction.

Concentric resonator consists of two spherical mirrors with the same radius R separated by a distance L=2R, so that the centers are coincident. The resonant frequencies use the same equation as above.

Confocal resonator consists of two spherical mirrors of the same radius of curvature R separated by a distance of L such that their foci F1 and F2 coincident. In this case, the center of curvature of one mirror lies on the surface of another mirror, L=R. The resonant frequency cannot be readily obtained from geometrical optics consideration.

Resonators formed by two spherical mirrors of the same radius of curvature R and separated by a distance L such that R<L<2R, i.e., inbetween confocal and concentric, are called Generalized Spherical Resonators, which is also often used.

Ring Resonator is a particularly important class of laser resonators. The path of the optical rays is arranged in a ring configuration or more complicated configurations like folded configurations. We can compute the resonant frequencies by imposing the constraints that the total phase shift along the ring path or the closed loop path must be equal to the integral numbers of 2p . Then the resonant frequencies are n = kc/Lp, where k is an integral number, Lp is the loop path length.

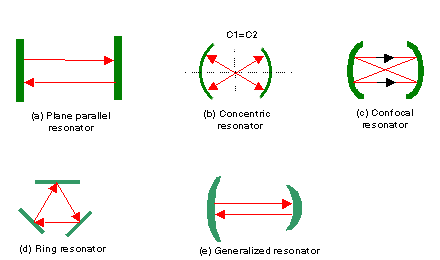
Figure 2.12: Various Resonators

(a) Plane parallel; (b) Concentric; (c) Confocal; (d) Ring; (e) General

Cavities can be identified as stable or unstable according to whether they make the oscillating beam converge into the cavity or spread out of the cavity. The output mirror of the laser resonator is finely coated to reach the required reflection into the cavity, if the beam is too intense, the mirror may suffer breakage. Breakage is serious because it causes shut down of the production. So for powers up to 2kW, lasers mainly use stable cavity designs(see figure ?a), laser output is from the center of optical axis. Stable cavity design allows the beam to oscillate many times inside the cavity to get high gain, the focal property and directionality are improved. For higher powered lasers, unstable cavities are often used (see figure ?b), laser output comes from the edge of the output mirror, which is often a totally reflecting metal mirror. The ring shaped beam reduces the intensity of the beam, thus reduces the risk of breakage. In the same time ring shaped beam is poor for focusing. Unstable cavities are suitable for high gain per round trip laser systems, which don’t require large numbers of oscillation between the mirrors.

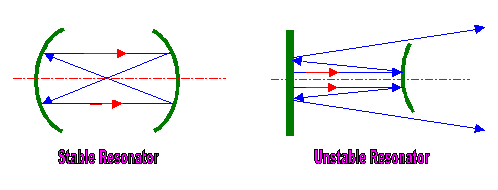
Figure 2.13: Stable and Unstable Resonators